Analysis Bootstrap¶
This tutorial shows how to perform analysis after A/B test experiments using bootstrapping. This technique makes inference about a certain estimate (e.g. sample mean) for a certain population parameter (e.g. population mean) by resampling with replacement from the observed dataset. It does not make any assumption on the samples distribution.
Let’s import first the tools needed.
[1]:
import numpy as np
import pandas as pd
from abexp.core.analysis_frequentist import FrequentistAnalyzer
from abexp.visualization.analysis_plots import AnalysisPlot
Simple bootstrap¶
Here we want to compare a specific metrics of the control group versus the treatment group (e.g. average revenue per user). We will perform bootstrapping on the kpi metrics (revenue) of each group.
[2]:
# Generate random data for revenue control group
revenue_contr = np.random.randint(low=50, high=500, size=100)
# Generate random data for revenue treatment group
revenue_treat = np.random.randint(low=50, high=600, size=100)
[3]:
# Define the analyzer
analyzer = FrequentistAnalyzer()
[4]:
# Define the aggregation function that will be applied on the sample
aggregation_func = np.mean
# other possibles aggregation functions might be:
# - standard deviation = np.std,
# - sum = np.sum
# - median = lambda x: np.median(x, axis=0)
Bootstrapping will generate a sequence of N values (where N is the number of repetitions). The bootstrap function returns a table with the median, 2.5 percentile and 97.5 percentile of this sequence.
[5]:
# Perform bootstrapping on the control group
stats_contr = analyzer.bootstrap(revenue_contr, func=aggregation_func, rep=500)
stats_contr
[5]:
| median | 2.5 percentile | 97.5 percentile | |
|---|---|---|---|
| 282.475 | 255.092 | 307.1285 |
[6]:
# Perform bootstrapping on the treatment group
stats_treat = analyzer.bootstrap(revenue_treat, func=aggregation_func, rep=500)
stats_treat
[6]:
| median | 2.5 percentile | 97.5 percentile | |
|---|---|---|---|
| 305.5 | 276.192 | 339.1205 |
[7]:
# Define heights of the bars
bars = [stats_contr['median'], stats_treat['median']]
# Compute the error between median and percentiles
ci_contr = [stats_contr['2.5 percentile'],
stats_contr['97.5 percentile']]
ci_treat = [stats_treat['2.5 percentile'],
stats_treat['97.5 percentile']]
[8]:
# Plot results with confidence interval
fig = AnalysisPlot.barplot(bars, [ci_contr, ci_treat],
groupslabel=['control group', 'treatment group'],
ylabel='average revenue per user', xlabel='')
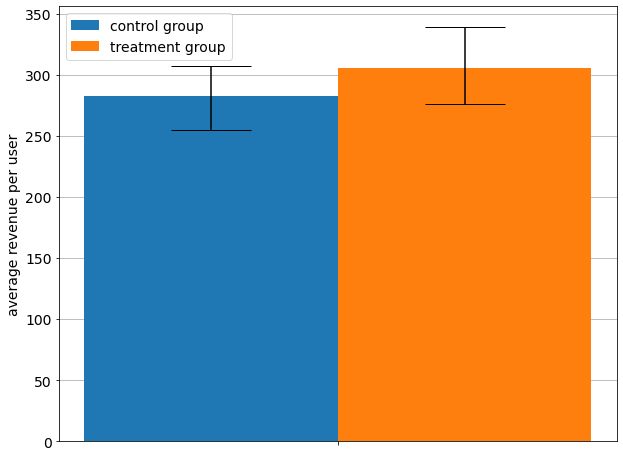
In the barplot above we see that there is no difference between empirical means because the confidence intervals overlap.
Time series bootstrap¶
Here we want to compare a specific metrics of the control group versus the treatment group (e.g. average revenue per user) across time. We will perform bootstrapping on the kpi metrics (revenue) of each group per each day. Note that the bootstrap function maintains the correlation across days.
[9]:
# Generate random data for revenue control group
revenue_contr_ts = pd.DataFrame({'day1': np.random.randint(low=1, high=500, size=1000),
'day2': np.random.randint(low=1, high=500, size=1000),
'day3': np.random.randint(low=1, high=500, size=1000),
'day4': np.random.randint(low=1, high=500, size=1000),
'day5': np.random.randint(low=1, high=500, size=1000),
'day6': np.random.randint(low=1, high=500, size=1000),
'day7': np.random.randint(low=1, high=500, size=1000)})
# Generate random data for revenue treatment group
revenue_treat_ts = pd.DataFrame({'day1': np.random.randint(low=1, high=600, size=1000),
'day2': np.random.randint(low=1, high=600, size=1000),
'day3': np.random.randint(low=1, high=600, size=1000),
'day4': np.random.randint(low=1, high=600, size=1000),
'day5': np.random.randint(low=1, high=600, size=1000),
'day6': np.random.randint(low=1, high=600, size=1000),
'day7': np.random.randint(low=1, high=600, size=1000)})
[10]:
# Perform bootstrapping on the control group
stats_contr_ts = analyzer.bootstrap(revenue_contr_ts, func=aggregation_func, rep=500)
stats_contr_ts
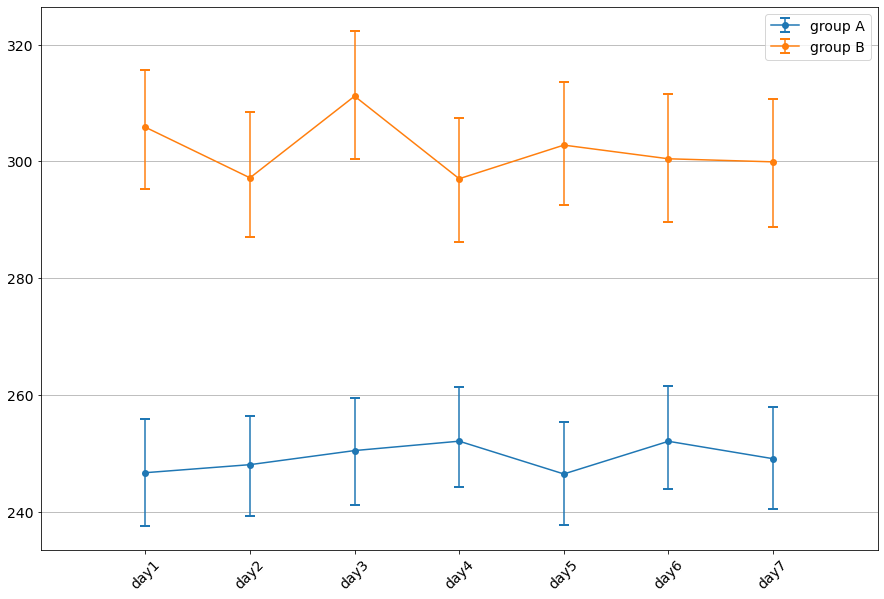
[10]:
| median | 2.5 percentile | 97.5 percentile | |
|---|---|---|---|
| day1 | 246.6630 | 237.597475 | 255.912150 |
| day2 | 248.0410 | 239.164575 | 256.451925 |
| day3 | 250.4535 | 241.068275 | 259.431525 |
| day4 | 252.0625 | 244.145850 | 261.326350 |
| day5 | 246.4465 | 237.647800 | 255.376150 |
| day6 | 252.0445 | 243.933075 | 261.501475 |
| day7 | 249.0605 | 240.451950 | 257.918600 |
[11]:
# Perform bootstrapping on the treatment group
stats_treat_ts = analyzer.bootstrap(revenue_treat_ts, func=aggregation_func, rep=500)
stats_treat_ts
[11]:
| median | 2.5 percentile | 97.5 percentile | |
|---|---|---|---|
| day1 | 305.8540 | 295.303525 | 315.689025 |
| day2 | 297.1785 | 287.122225 | 308.437950 |
| day3 | 311.1690 | 300.329400 | 322.258075 |
| day4 | 297.0245 | 286.180500 | 307.432525 |
| day5 | 302.7850 | 292.530300 | 313.642875 |
| day6 | 300.4425 | 289.563675 | 311.556775 |
| day7 | 299.9155 | 288.822375 | 310.642600 |
Plot results with confidence intervals
[12]:
# Define heights of the bars
y = [stats_contr_ts['median'], stats_treat_ts['median']]
# Compute the error between median and percentiles
ci_treat_ts = [stats_treat_ts['median'] - stats_treat_ts['2.5 percentile'],
stats_treat_ts['97.5 percentile'] - stats_treat_ts['median']]
ci_contr_ts = [stats_contr_ts['median'] - stats_contr_ts['2.5 percentile'],
stats_contr_ts['97.5 percentile'] - stats_contr_ts['median']]
[13]:
fig = AnalysisPlot.timeseries_plot(y, [ci_contr_ts, ci_treat_ts])